分数混合数計算ツール

混合数とは、2 ½や5 ¾のようなもので、単なる学校の数学問題以上のものです。これはレシピの記述方法であり、木材の販売単位であり、スポーツでの距離の測定にも使われています。

混合数と仮分数の違い

もしあなたが2 ½カップの小麦粉を計量したことがあったり、誰かが5 ¾マイル走ったと言ったのを聞いたことがあれば、それはすでに混合数を扱った経験があるということです。混合数は整数と真分数（適切な分数）が組み合わさったもので、例えば3 ½は3つの整数部分と半分を合わせたものです。これらは実用的で身近なもので、私たちが日常的に思っている以上に使われています。

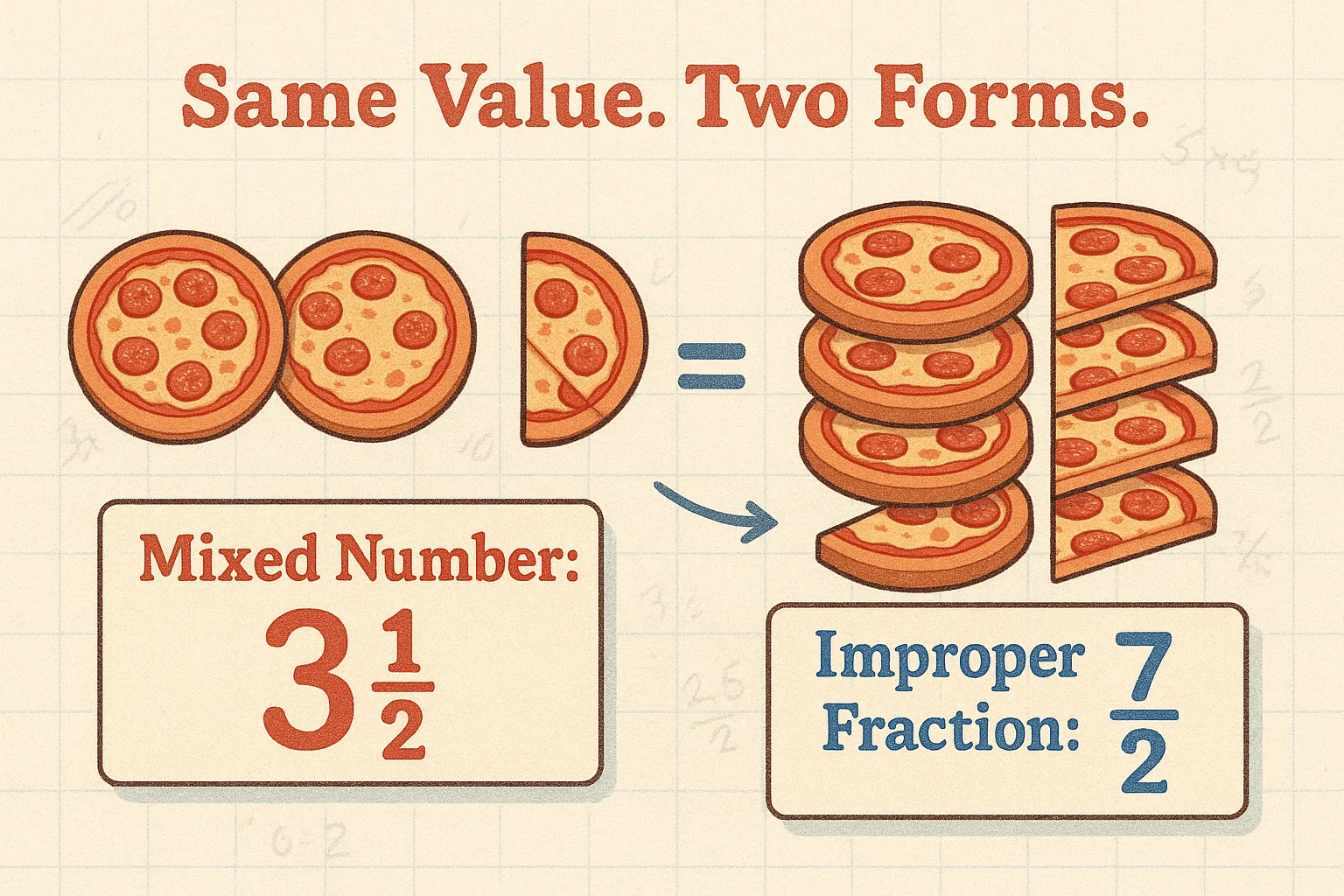
一方、仮分数は少し見た目が複雑ですが、数学的には同じものです。仮分数とは、分子（上の数）が分母（下の数）と同じかそれ以上の値を示す分数のことで、たとえば⁷⁄₂です。これは3 ½と同じ値ですが、表記が異なります。

なぜ同じものに対して2つの表現を使うのか？混合数は一目でわかりやすいため人間にとって理解しやすい一方、仮分数は特に代数やプログラミングの計算では扱いやすいからです。

混合数から仮分数への変換方法:

たとえば4 ⅗があるとします。

1. 整数部分と分母を掛けます：4 × 5 = 20

2. 分子を足します：20 + 3 = 23

3. 元の分母を分母にして表記：²³⁄₅

つまり4 ⅗は²³⁄₅になります。

これは混合数を乗算や除算する前に仮分数に変換する際の一般的な手順です。

仮分数から混合数への変換方法:

例として¹¹⁄₄を使います。

1. 分子を分母で割ります：11 ÷ 4 = 2 余り3

2. 商が整数部分（2）、余りが新しい分子（3）です。

3. 元の分母はそのまま保持します：2 ¾

これが仮分数から混合数に戻す方法です。

豆知識：「アポロ13号のミッション中、NASAのエンジニアはスライドルールと分数（例：2 ⁵⁄₈）を使った手計算で宇宙船の軌道修正を迅速に行い、乗組員を救いました。」 — NASAアーカイブ¹

分数混合数の計算方法

混合数の加算、減算、乗算、除算では、整数部分と分数部分の両方を扱う必要があります。ポイントは、計算をシンプルかつ明確にし、必ず結果を約分することです。レシピの分量を倍にする場合でもテスト問題を解く時でも、これらのルールを知っていれば素早く正確に計算できます。

加算と減算

まず整数部分と分数部分を分けて計算します。混合数は両方を含むので、それぞれ個別に計算した後、最後に合わせます。

例を見てみましょう：

加算：2 ½ + 3 ¾

1. 整数部分を足す：2 + 3 = 5

2. 分数部分を足す：½ + ¾ → 通分 → ²⁄₄ + ³⁄₄ = ⁵⁄₄

3. 総和は 5 + ⁵⁄₄ → ⁵⁄₄ = 1 ¼なので、答えは:
   → 6 ¼

減算：5 ⅚ − 2 ⅔

1. 整数部分：5 - 2 = 3

2. 分数部分：⁵⁄₆ − ²⁄₃ → ²⁄₃を⁴⁄₆に通分 → ⁵⁄₆ − ⁴⁄₆ = ¹⁄₆

3. 答え：3 ¹⁄₆

引き算で分数部分が負の値になる場合（例：¼ − ¾）、整数から借りる必要があります。ここを省くとミスが生まれやすいので注意しましょう。借りるべきか迷ったら分数約分ツールで結果を確認すると良いでしょう。

乗算

混合数の乗算は必ず仮分数に変換してから始めます。

例：2 ⅓ × 1 ½を計算するとします。

1. 両方を仮分数に変換：
   2 ⅓ = ⁷⁄₃
   1 ½ = ³⁄₂

2. 分子同士・分母同士を掛ける：
   ⁷⁄₃ × ³⁄₂ = ²¹⁄₆

3. 約分：
   ²¹⁄₆ = 3 ½

これで計算完了です。

事実：「シカゴの高校の研究で、混合数を乗算前に仮分数に変換する練習をした生徒は、視覚的に推測していた生徒に比べて27％テストの成績が向上した」 — 米国教育省調査²

乗算は分母を揃える必要がないため、加減算よりも扱いやすいです。結果の正確さに不安があれば、まず紙で手計算し、その後分数計算ツールで検算してみてください。

除算

除算は苦手意識がありますが、実際は乗算の一種です。

例えば、3 ¾ ÷ 1 ½を計算しましょう。

1. 仮分数に変換：
   3 ¾ = ¹⁵⁄₄
   1 ½ = ³⁄₂

2. 割る方の分数を逆数にする：
   ³⁄₂ → ²⁄₃

3. 乗算：
   ¹⁵⁄₄ × ²⁄₃ = ³⁰⁄₁₂

4. 約分：
   ³⁰⁄₁₂ = 2 ½

これが「逆数にして掛ける」という方法です。

結果が仮分数（例：²¹⁄₄）の場合、代数式や正式な文章ではそのまま使い、日常では混合数（5 ¼）に直すことが多いです。

教室でもキッチンでも、これらの計算方法を理解していると、どんなに複雑な分数でも自信を持って扱えます。不安な時は数学計算ツールで確認もできます。

分数が現場を救った話

混合数は教室だけでなく、現場でも時間や費用、プロジェクト全体を救うことがあります。

アイオワ州デモインの建設現場監督は、ある学校改装工事で起きた失敗談を共有しました。設計図にはカスタム金属トリムの寸法が8 ⅜インチと記されていましたが、新人の見習いが10進数の8.3インチと誤読しました。その結果、アルミパネルが約¹⁄₁₆インチ短くなり、検査に不合格となったのです。

このミスで作業のやり直しに1週間と材料費4,000ドル以上が余計にかかりました。

「小数は必ずしも味方ではないと痛感しました。実際の目盛りは分数で表されている。⅜と0.375では大きな違いがあり、給料に影響します。」— ティム・ベガ、Vega & Sons Build Co. 建設担当⁴

現在は、製造工場に送る寸法は必ず分数と小数の換算表を道具箱に貼り付けて確認し、新人には分母を通分して混合数の加減算を教えるようにしています。

混合数は単なる学問のためのものではありません。設計図、レシピ、請求書、スポーツ統計、器具の調整など、あらゆる場面で使われます。習得しておけば、実際の現場で自信をもって数値を扱えます。

1. NASA. “Apollo 13 Timeline.”

2. 米国教育省. “高校数学研究.”

3. Napa Valley College ベーキング＆料理プログラム、2023年3月の経験談インタビュー

4. ティム・ベガ氏インタビュー、2022年6月。アイオワ州公共安全局 建築基準・検査担当