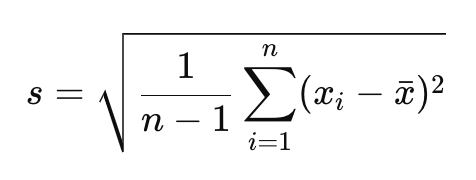標準偏差計算ツール

標準偏差は、学校の授業や研究報告書などで耳にしたことがある用語かもしれません。しかし、この一見難しそうな名前の背後には、科学的発見からビジネス戦略、天気予報に至るまで幅広く活用される、驚くほど直感的な概念があります。簡単に言えば、それはデータの散らばり具合―平均からどれだけ離れているか―を理解する手段です。変動性を測ることで、日々使うデータに対して明確性、文脈、そして自信を得られます。

詳しい計算ツールは数学をご覧ください

標準偏差とは何か？

標準偏差は、データセット内の値がどれだけ散らばっているかを示します。つまり「値が平均からどれだけ離れているか」を数値で表す方法です。

例えば、先生が100点満点の小テストを実施し、クラス全員がちょうど80点だったとします。この場合、平均は80で全員の得点も80なので、標準偏差はゼロ。データに変動はありません。次に、平均が同じ80点でも得点が60点、70点、90点、100点とばらついているクラスを想像してください。平均はやはり80ですが、点数は大きく散らばっています。このクラスの標準偏差は、先ほどのクラスよりずっと大きくなります。

標準偏差が小さいときはデータが平均付近に密集し、大きいときはより広範囲に散らばっていることを意味します。

なぜデータの変動性が重要なのか？

変動性は単なる統計的ノイズではなく、データが語るストーリーです。標準偏差でデータの揺らぎを測ることで、トレンドや異常値、潜在的パターンを見つけられます。医療分野では治療効果の一貫性を評価し、気候科学では気温の異常変動を追跡します。教育では学校間の生徒成績の比較に、エンジニアリングでは品質管理に活用されます。変動性を把握せずにデータを解釈すると、本来の意味を見誤るリスクがあります。

関連ツールを試す：平均値計算ツール、分散計算ツール、Zスコア計算ツールでさらにデータのストーリーを探りましょう。

母集団標準偏差

調査対象の全データを持っている場合は、母集団標準偏差を算出できます。この方法では推定が不要で、例えば全員のデータやアンケート全回答を使って、母集団全体の散らばりを正確に把握できます。

母集団標準偏差の公式：

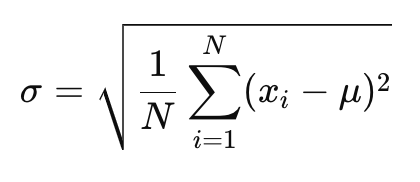
ここで、

𝜎：母集団標準偏差

𝑁：データの総数（母集団の大きさ）

x_i：各データ点の値

𝜇：母集団の平均

標本標準偏差

母集団全体のデータを取得できない場合、標本データを基に母集団標準偏差を推定します。標本標準偏差には推定偏りを補正する調整が含まれ、散らばりを過小評価しないようにしています。

標本標準偏差の公式：

ここで、

𝑠：標本標準偏差

𝑛：標本の観測数

x̄：標本の平均

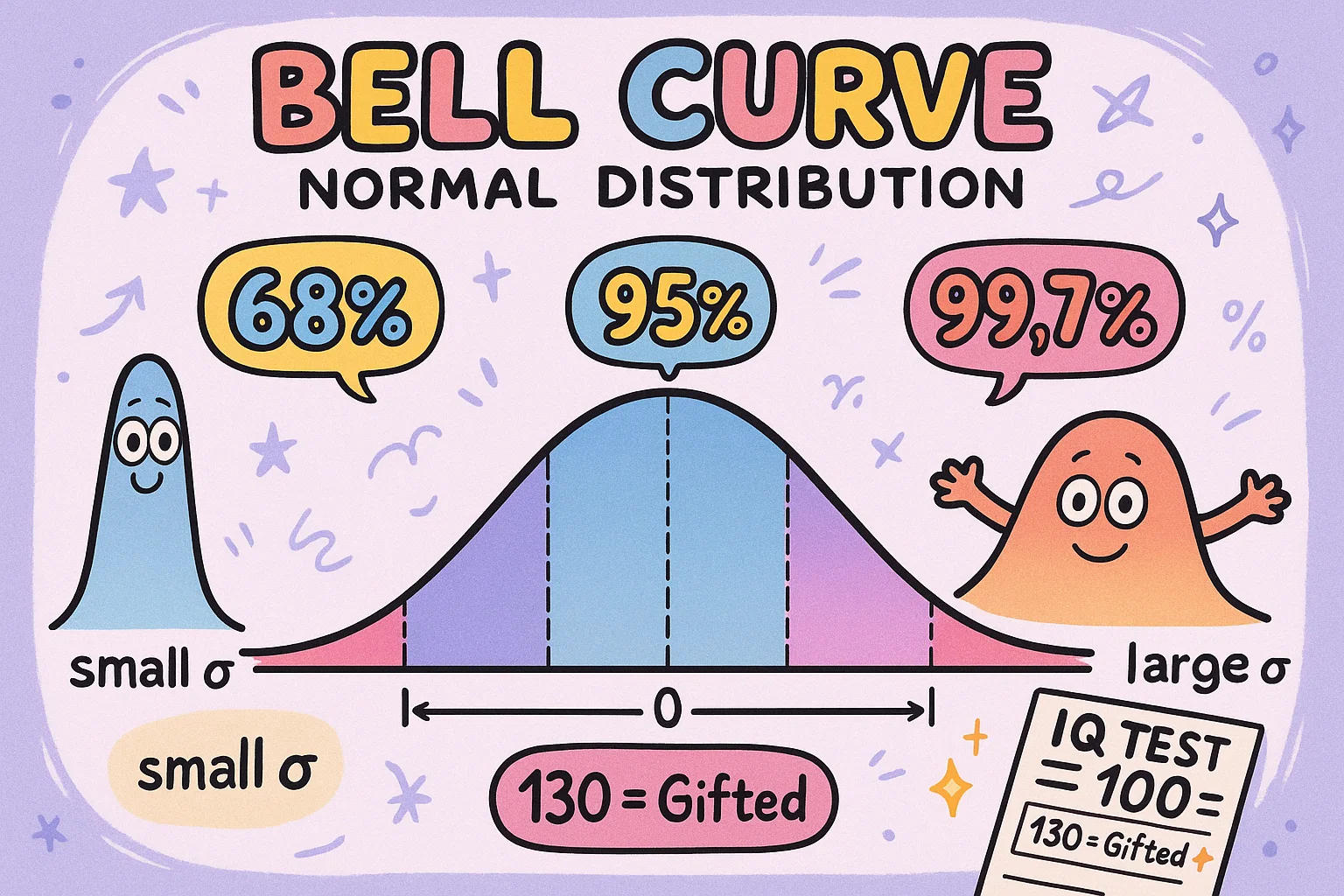
ベル曲線と正規分布

ベル曲線（滑らかな丘の形）をご覧になったことがあるでしょう。中央に値が集中し、両端に行くほど少なくなるグラフです。これが正規分布と呼ばれ、身長、IQ、テスト結果、血圧など、さまざまな実世界のデータに現れます。

ここで標準偏差の出番です。曲線がどれだけ広がるかは標準偏差で決まります。数値が平均付近に密集すれば高く尖った曲線（標準偏差小）、広く散らばれば低く横に広がる曲線（標準偏差大）になります。

便利なルールがあります：

• 平均から1標準偏差以内に約68％の値が収まる

• 2標準偏差以内に約95％

• 3標準偏差以内に約99.7％

このルールを使えば、テストの点数や株価の変動が典型的か異常かを簡単に判断できます。

🎯 面白豆知識：多くのIQテストは平均100、標準偏差15のベル曲線に合わせて設計されています。そのためIQ130はギフテッドと見なされます。