立方根計算ツール

立方根計算ツールは、正の数の立方根(3乗根)を求めたい方に欠かせないツールです。この汎用ツールは、立方根の算出を簡素化するだけでなく、数値の3乗計算も手軽に実行できます。数学の問題を解いたり、完全立方数を見つけたり、他の次数の根を計算したりする際にも、立方根計算ツールが正確かつ高速な結果を提供します。
立方根とは何か?
数の立方根とは、その値を3回掛け合わせたときに元の数になる値のことです。数式では ³√x = y と表し、y³ = x を意味します。
または、次のようにも書けます:³√x = x^(1/3)
例えば27の立方根を求める場合、y³ = 27 となる数を探します。答えは 3 で、3 × 3 × 3 = 27 となります。この概念は算術や代数、さらにはより高度な数学にも基本的な役割を果たします。
立方根の幾何学的解釈
立方根には空間的な解釈もあります。容量が27立方センチメートルの立方体を想像してください。一辺の長さを求めるには27の立方根を計算します。すると一辺の長さは3cmとなり、3³ = 27 が成り立ちます。
この実用的なつながりにより、立方根は幾何学、工学、建築学、製品設計などで三次元空間を理解するうえで非常に重要です。
二次元デザインの関連計算には、正方形面積計算ツールをご利用ください。
完全立方数とは?
完全立方数は整数を3乗して得られる数です。これらを把握しておくと、問題解決が一層スムーズになります。以下はよく使われる例です:
これらの値は幾何学、物理学、数学での参照や計算時に頻繁に利用されます。完全立方数を見分けることで、立方根計算や整数の3乗表現の判定が容易になります。
| 数値 | 完全立方数 |
|---|---|
| 1³ | 1 |
| 2³ | 8 |
| 3³ | 27 |
| 4³ | 64 |
| 5³ | 125 |
| 6³ | 216 |
| 7³ | 343 |
| 8³ | 512 |
| 9³ | 729 |
| 10³ | 1,000 |
立方根関数とそのグラフ
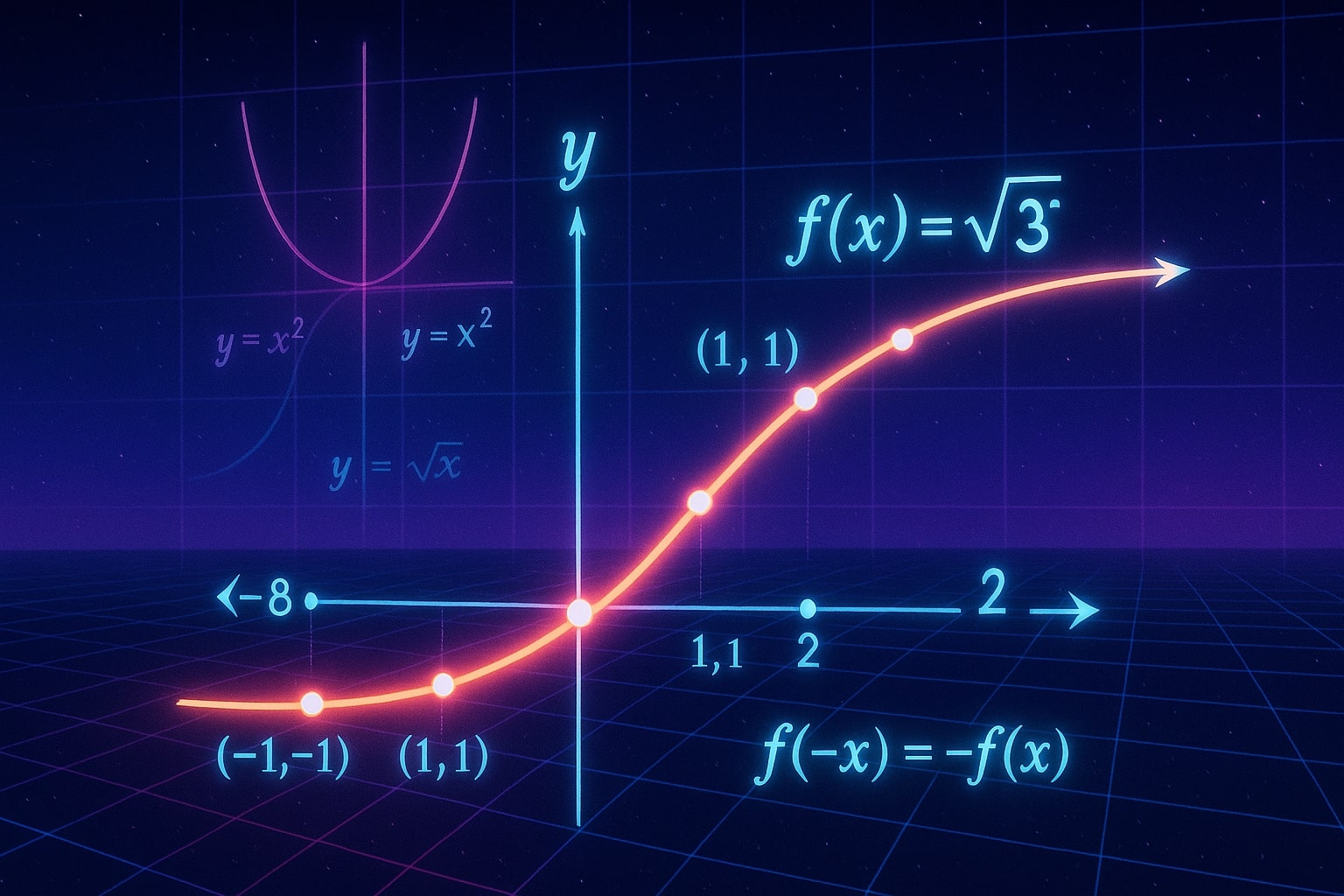
立方根関数は f(x) = ³√x と表され、原点を中心に回転対称性を持つ奇関数です。この性質は次の式で表されます:
f(−x) = −f(x)
立方根関数の特徴:
- 原点を通過:グラフは (0, 0) を通ります。
- 定義域と値域:ともに全実数 (ℝ) です。
- 挙動:x が正の無限大に近づくと y も増加し、逆に x が負の無限大に近づくと y は減少します。
³√x = y のグラフは緩やかなカーブを描き、二次関数や平方根関数のような急激な変化とは異なる滑らかな変化を示します。
二次元版と比較するには、平方根計算ツールをお試しください。
他にも多数のツールをご用意しています。ぜひ数学計算ツールの全ラインナップをご覧ください。
