長方形面積計算ツール

長方形は、数学だけでなく日常生活でも最もよく知られている形の一つです。庭のレイアウトから建築計画、教室の幾何学の問題まで、長方形の面積を正確かつ効率的に計算するスキルは不可欠です。このガイドでは、長方形面積計算ツールの使い方を紹介しながら、公式の意味、実生活での応用例、興味深い豆知識や歴史的な失敗談に触れていきます。最後には実用的な自信と、幾何学が現実世界でどのように活用されているかの理解が深まるでしょう。

他の形についてもっと知りたいですか？当社の面積計算ツールコレクションもぜひお試しください。

長方形とは何か

長方形と聞くと、本や窓、スマートフォンの画面など日常的な物が思い浮かびます。長方形は身近すぎて、その面白さを見過ごしがちです。

幾何学では、長方形は全ての角が90度の四辺形に分類されます。長方形の特徴は、対辺が等しい長さで完全に平行になっていることです。正方形を一方向に引き伸ばした形が長方形だとイメージしてください。

長方形は何千年もの間、多くの文明で利用されてきました。古代の建築家たちは、壁や神殿を造る時に長方形の石材を選び、その形のバランスと安定性を頼りました。現代のエンジニアや建築家も、対称性が計算を簡単にし、強固なデザインを支えるため長方形を好んで使っています。

長方形をイメージする簡単な方法は、タイル張りの床を思い浮かべることです。タイル一枚が全体の一部を表し、等しい正方形の単位で覆われた面を想像することで、面積の基本的な考え方が理解できます。

単純に見えても、長方形は建築、画面設計、芸術、工学、物理などさまざまな分野で重要な役割を果たしています。長方形の仕組みを理解することで、デジタルや物理的な環境の幾何学的パターンを見る視点が広がります

他の形との比較が気になりますか？完全な辺の長さを持つ図形の面積を探索するには正方形面積計算ツール、傾いた四辺形を調べるには平行四辺形面積計算ツールをお試しください。

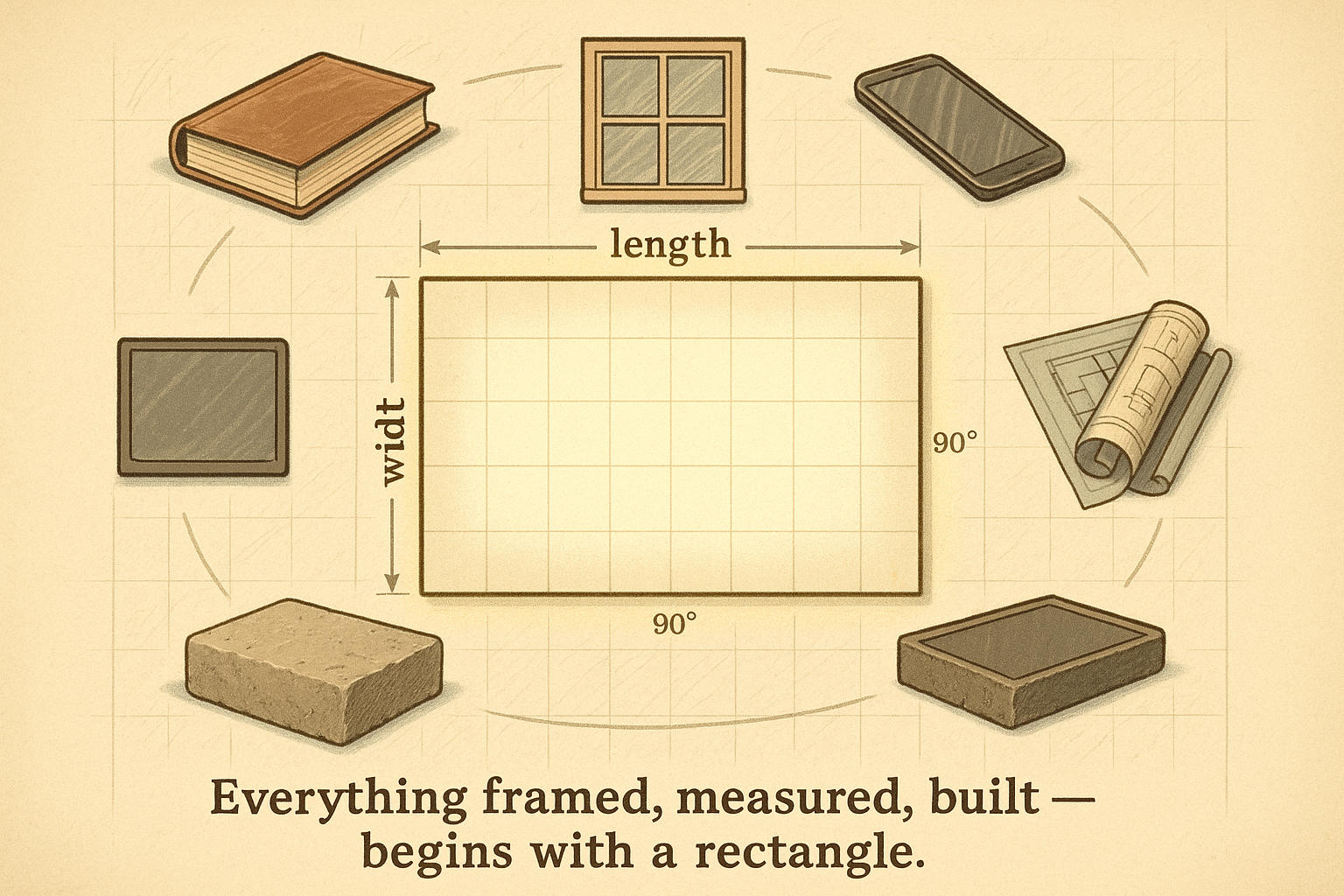
長方形の面積をどう計算するか？

多くの人が最初に学ぶ幾何学のスキルの一つは長方形の面積の計算方法です。このスキルは非常に役立つため忘れにくいものです。床材の概算や壁紙の寸法測定など、基本的な計算が時間と労力を大幅に節約します。

基本的な公式は：

面積 = 長さ × 幅

ここで：

• 長さ： 長方形の長い方の辺

• 幅： 長方形の短い方の辺

• 結果： 平方メートル、平方フィート、平方インチなどの平方単位で表します

具体的な手順：

ステップ1： 長さと幅を測る

定規やメジャーを使って長方形の2辺を測り、正確に記録します。

例： 机の長さは5フィート、幅は3フィートです。

ステップ2： 両方の測定が同じ単位になっていることを確認する

計算前に長さと幅が同じ単位で測定されているかをチェックします。

• 1メートル = 100センチメートル

• 1フィート = 12インチ

単位変換が必要な場合は、当社の面積計算ツールを使って測定値を統一してください。

ステップ3： 公式を適用する

長さと幅を掛け合わせます。

ステップ4： 面積を平方単位で表示する

使用した入力単位に応じて結果はm²、ft²、in²などになります。

ポイント： 単位を必ず再確認しましょう。小さなことですが、正しい面積を得るためには大きな違いになります。

この手順を理解すれば、床面積の概算や包装設計、学術問題の解決など、さまざまな場面で役立つことに驚くでしょう。

大失敗の舞台事故

1959年、ブロードウェイの制作チームが、バックステージにぴったり収まる長方形のステージ台を設計しました。サイズは長さ30フィート、幅20フィートの予定でした。しかしチームの誰かが幅の測定を読み間違え、フィートではなくインチで計算してしまいました。

結果として、ステージ台は約2フィートも幅が広くなりました。

最終リハーサル時、チームはステージ台を所定の位置に滑り込ませようとしましたが、入口で詰まってしまい、出演者や小道具の通行を妨げてしまったのです。開幕の数時間前にバックステージが大混乱に陥りました。

急きょ過剰部分を切り落とし、塗り直し、台を再調整する作業を徹夜で行いました。

注意： 長方形の寸法と単位は必ず二重に確認しましょう。