扇形面積計算ツール

曲線を活かした庭園のレイアウトから円形劇場の設計まで、扇形の面積は円形空間の計画において重要な概念です。本ガイドでは円の幾何学の基本を理解し、実際の利用例を紹介し、さらに興味深い豆知識もご紹介します。

他の形状についても知りたいですか？当サイトの豊富な面積計算ツールコレクションをご活用ください。

扇形の面積とは？

扇形とは円の一部であり、ピザの一切れや円グラフのひと区画、円形の花壇の一部のような形状です。これは2本の半径とそれらの間の弧で構成されます。扇形の面積とは、この“一切れ”の面積のことであり、通常は平方フィートで表します。

円全体は360度なので、扇形の大きさは円の半径と、その“一切れ”の角度によって決まります。例として、90度の扇形は円全体の4分の1に相当します。

この概念は、円形噴水の配置やレーダーの範囲設定、劇場の舞台上でのスポットライトの照射範囲の計算など、実際のさまざまな場面で活用されています。

💡 豆知識：NASAは衛星の地球上の信号カバレッジ計画時に扇形面積の公式を用いています。衛星の多くは円形または放射状のパターンで信号を送信するため、扇形の面積を計算することで通信範囲の重複を防ぎ、最適な衛星配置を実現しているのです。

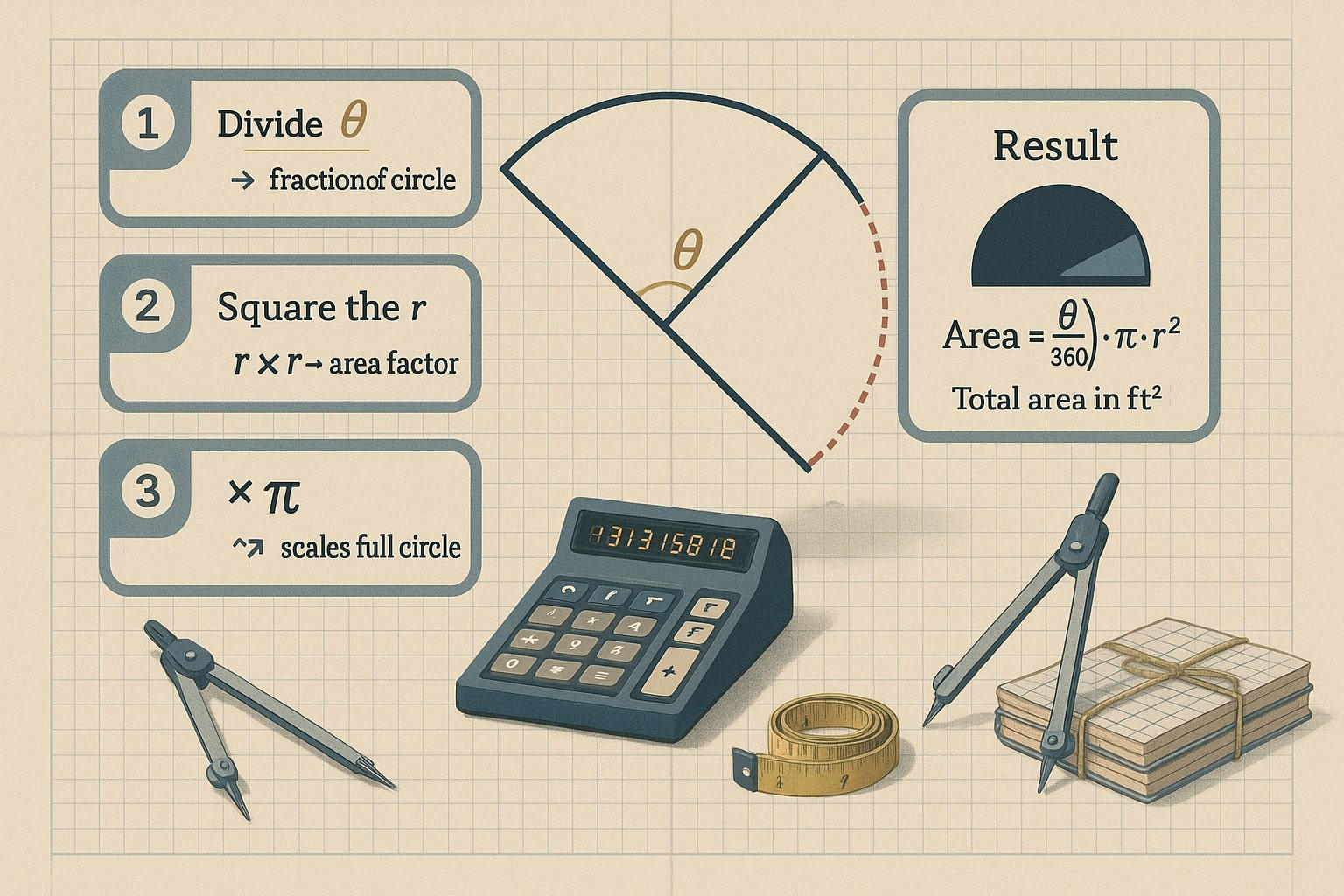
扇形の面積の計算法（例付き）

扇形の面積を求めるのは思っているより簡単です。必要なのは次のシンプルな公式だけです：

扇形の面積 = (θ ÷ 360) × π × r²

各項の意味を説明します：

• θ は扇形の中心角（度数法）

• r は円の半径（中心から円周までの距離）

• π は定数で約 3.1416

この公式は、円全体が360度であることを踏まえ、「角度÷360」で扇形が円全体の何分の何かを示す割合を計算しています。

例：半径6フィートの円形花壇において、120度の扇形の面積を求めてみましょう。

ステップ1：数値を確認

• 半径 (r) = 6フィート

• 角度 (θ) = 120度

ステップ2：公式に当てはめる
面積 = (120 ÷ 360) × π × (6²)
= (1/3) × π × 36
= π × 12
≈ 3.1416 × 12
≈ 37.7平方フィート

つまり、その扇形はあなたの花壇の約37.7平方フィートを占めることになります。

扇形、長方形、その他の形状を組み合わせた複雑なレイアウトでは、面積計算ツールを使うことでより正確な合計面積を求めることができます。

京都の円の庭園

静かな壁に囲まれた京都のあまり知られていない禅寺の裏手に、一般の庭園とは一線を画す場所があります。地元で「円の庭（えんのにわ）」と呼ばれるこの庭は、一見するとなだらかに配された石や苔、砂利の弧線が静寂な水面の波紋のように広がっています。しかし、この落ち着いた設計の背後には、何世紀も前から続く円の幾何学の深い応用があります。

この庭は禅の円相（えんそう）を象徴に取り入れており、円は悟り、完全性、生命の循環を表します。1600年代後半の再設計時には、寺の記録にあるように、僧侶たちが巧みな庭師と協働し、手描きの扇形図を使用して弧線の配置を緻密に計画しました。各曲線の幅を計算し、視覚的なバランスと調和を保つように配慮されていました。

当時は「扇形の面積」という言葉は使われていませんでしたが、基本的な考え方は同じです。角度と半径を測定し、苔や砂利の各区画が正確な面積を占めるようにし、庭全体にリズミカルで瞑想的な流れを作り出していました。その美しさは寺の瞑想用の見晴らし台からの一点透視で最もよく感じられます。

数学セクションで簡単かつ迅速に数学問題を解く方法をチェックしましょう