楕円体体積計算ツール

半軸の値を使って楕円体の体積を計算できる楕円体体積計算ツールです。数学、物理、工学の分野での利用に適しています。

埋め込む

正直に言うと、「楕円体」は日常会話であまり使う言葉ではありません。しかし驚くべきことに、楕円体は私たちの周りにたくさんあります。卵をそっと抱えたり、ラグビーボールを投げたり、宇宙から地球を見たりしたことはありませんか？それがまさに楕円体の例です。円錐や角錐などのあらゆる３次元形状については、メインの体積計算ツールページにまとめています。

楕円体とは何か？

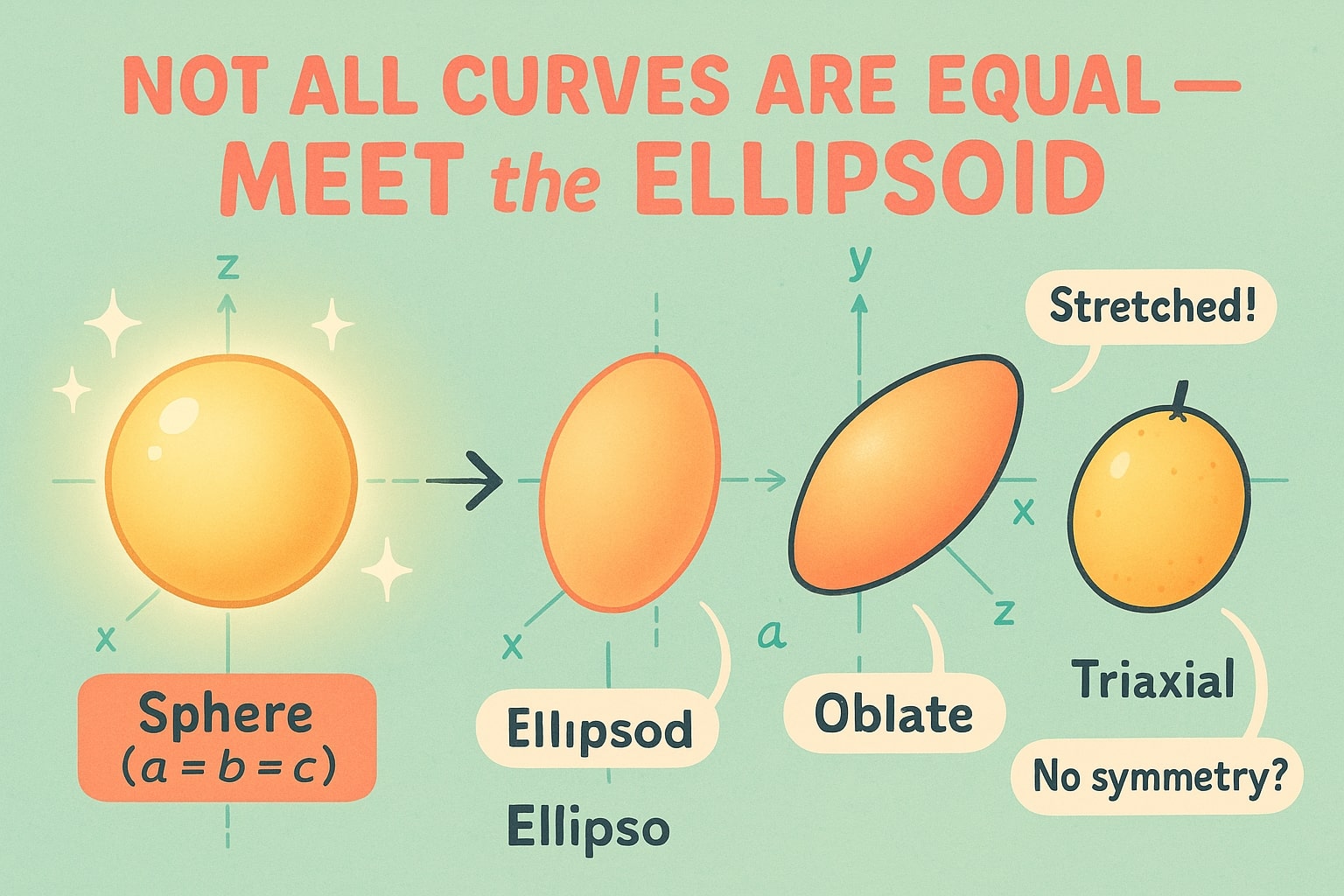
まずは球体を想像してください——完全な丸い３次元の物体です。そこからそっと押しつぶしたり横に引き伸ばしたりした形。そのなめらかで丸みはあるが、全方向で同じではない形状が楕円体です。

幾何学的に楕円体は次の３つの軸で表されます：

a = x軸方向の長さ
b = y軸方向の長さ
c = z軸方向の長さ

もしa、b、cが全て等しければ、それは球体です。しかし異なる場合は楕円体となります。

よくあるタイプは以下の通りです：

伸長楕円体（プロレート楕円体）： １つの軸に沿って伸びた形（ラグビーボールのような形）
扁平楕円体（オブレート楕円体）： １つの軸に沿って押しつぶされた形（地球のような形）
三軸楕円体： ３つの軸すべてが異なる形（対称性がなく、不規則な果物や医療用カプセルのような形）

惑星の形から細胞、魚の卵まで、楕円体は思った以上に身近に存在します。だから楕円体の体積を計算できることは非常に役立ちます。

楕円体体積計算ツール 1

体積を計算した後は、体積単位変換ツールを使ってリットルやガロンなど、他の単位にすばやく変換できます。

楕円体の体積の計算方法

朗報です：体積の計算式は意外とシンプルです。３つの半軸の長さ（a、b、c）がわかれば、次の式に当てはめるだけです：

体積 = (4/3) × π × a × b × c

これだけです。３つの半軸を掛け合わせ、それにπ（パイ）をかけ、さらに4/3をかけます。

ワンポイント： 直径ではなく半軸を使うことを忘れないでください。楕円体の幅が10cmなら、計算には半分の5cmを使います。

例えば半軸が4cm、3cm、2cmの楕円体の場合、
体積は次のように計算します：

体積 = (4/3) × π × 4 × 3 × 2 = (4/3) × π × 24 ≈ 100.53 cm³

もし３つの半軸が全て５cmで等しい場合は、その楕円体は実際には球体です。この場合は定番の球の式が簡単に使えます：

体積 = (4/3) × π × r³

💡 プロのコツ： 形状がほぼ球体なら、球の体積の式で近似計算できます。あるいは当サイトの球体体積計算ツールを使うと便利です。

ガウスと地球の形状

19世紀初頭、まだ衛星もGoogle Earthもなかった時代に、ドイツの数学者カール・フリードリヒ・ガウスが大胆な問いかけをしました：地球の本当の形は何か？

楕円体体積計算ツール 2

多くの人が地球は完全な球体だと考えていました。しかしガウスは違和感を抱いていました。地球は極で少し扁平になっている、つまり今でいう扁平楕円体だと疑ったのです。彼はただ理論を唱えるだけでなく、山に登り、機材を運び、新しい測定技術を開発して非常に高精度な距離測定を実現しました。

この先駆的な努力により、地球の形状と大きさを研究する測地学が確立されました。そして彼の予測は正しく、地球は完璧に丸くなく、赤道部分で膨らみ、極部で平らになっています。この細かな違いは衛星システムの設計や正確な位置座標の計算において非常に重要です。

楕円体に関する豆知識

地球は完全な球体ではありません——それは扁平楕円体で、赤道が少し広がっています。違いはわずか数ミリメートルですが、GPSや宇宙航行のためには重要な意味を持ちます。
卵は自然界の近似楕円体です。完全ではないものの、鶏の卵は楕円体に非常に近く、農業研究ではその体積を予測するのに楕円体の計算式が使われています。
多くの宇宙の岩石や衛星は楕円体状で球体ではありません。これは重力が十分強くなく、完璧な球体に形成されないためです。
医療画像でも楕円体形状が活用されています。MRIや超音波検査では、臓器の体積を楕円体近似で推定し、完全な３Dスキャンをせずに効率的に測定が行われています。