分数基本計算ツール

分数はレシピ、建築、税金、さらにはピザの分け合いまで、あらゆる場面に登場します。分数計算を得意にすれば時間を節約し、ミスを防ぎ、学生からプロまで自信を持って取り組めます。⅔ + ¼ の足し算から ⅝ × ¾ の掛け算まで、本ガイドでは手順を分かりやすく解説し、よくある混乱を解消し、実生活の問題とのつながりを示します。

分数とは？

分数は全体の一部を表す方法です。上下に数字を並べ、中央に線を引いて書きます。上の数が分子（持っている部分）、下の数が分母（全体をいくつに分けたか）になります。

ピザを例に考えてみましょう。8 等分されたピザを3切れ食べたら、3/8 を食べたことになります。3があなたの切れ数、8がピザ全体です。

分数は数学の授業だけでなく日常でもよく使われます。レシピでは砂糖½カップや塩¾小さじ。建築や測定では厚さ5/8インチの板など。友人と割り勘をしたり、割引率を計算したりするときにも出番があります。

日常で見かける例：

• パイの半分：½

• ガソリンタンクの3/4：¾

• 定規の5/8インチ：5⁄8

分数があれば、整数に収まらない量も柔軟に表現できます。

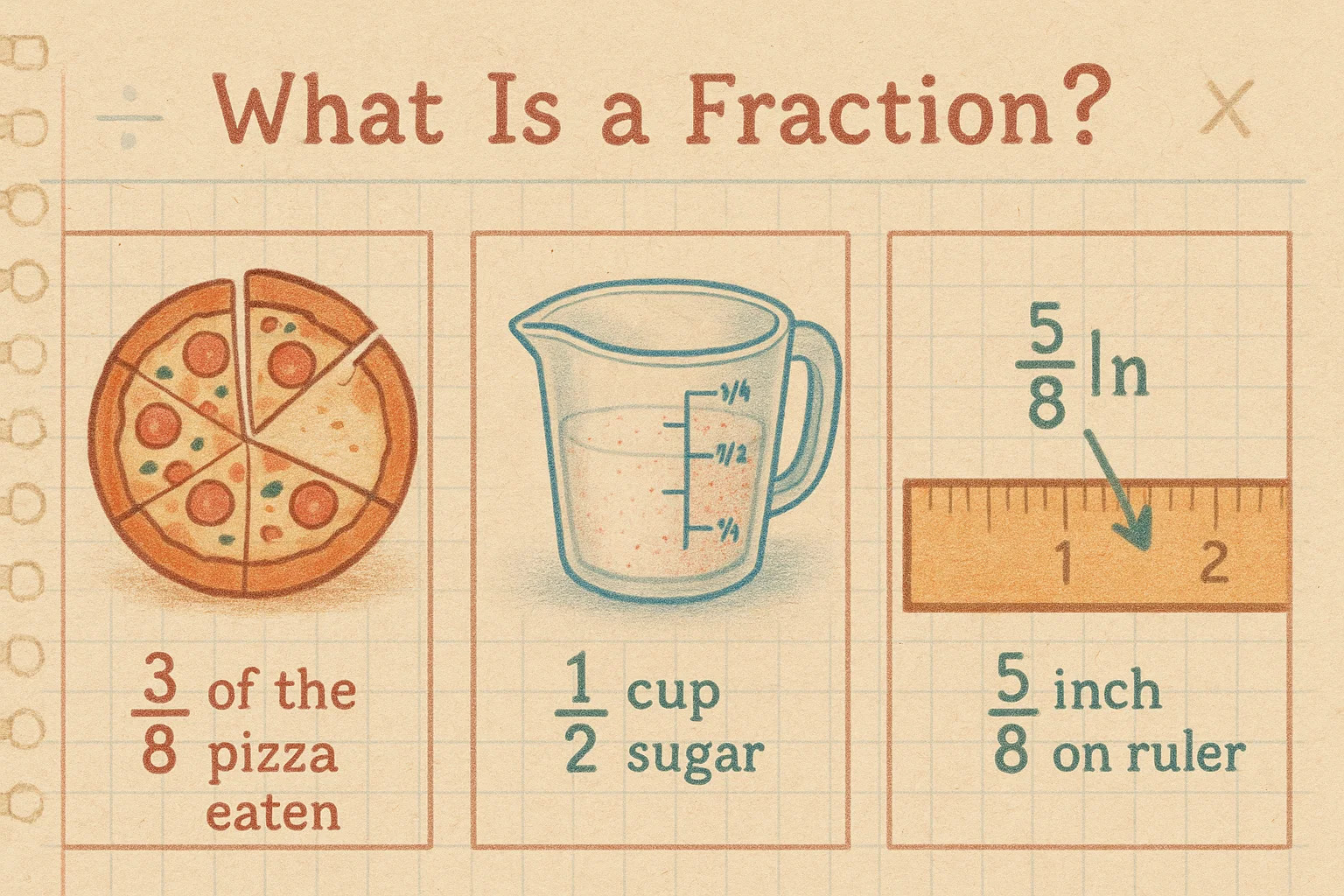
分数の足し算

分母が同じ分数同士の足し算は簡単です。分子同士を足して、分母はそのままにします。

例：1⁄4 + 2⁄4 = 3⁄4

分母が異なる場合は、先に最小公倍数（LCM）などで通分して分母をそろえてから計算します。

異なる分母の例：1⁄3 + 1⁄6

• 最小公倍数は6。

• 1⁄3 を 2⁄6 に書き換える。

• 2⁄6 + 1⁄6 = 3⁄6。

• 3⁄6 は3で約分して½。

手早いコツ：分母の一方がもう一方の倍数なら、最小公倍数を求めずに大きい方の分母で通分できます。

分数の引き算

引き算も足し算とほぼ同じ手順ですが、符号がマイナスになります。

分母が同じなら分子同士を引いて、分母はそのままにします：

5⁄8 − 3⁄8 = 2⁄8 で1⁄4に約分。

分母が異なる場合は最小公倍数で通分してから引き算します：

例：5⁄6 − 1⁄3

• 最小公倍数は6。

• 1⁄3 を 2⁄6 に書き換える。

• 5⁄6 − 2⁄6 = 3⁄6。

• 3⁄6 は½に約分。

小さい方の分数を調整後に分子が大きい場合、結果は負になります。例：
1⁄4 − 3⁄4 = −2⁄4 = −½。

補足：結果を帯分数で表しても構いませんが、不適切分数（−5⁄4）のままでも多くの問題で受け入れられます。

分数の掛け算

掛け算は最もシンプルな操作です。通分は不要で、分子同士、分母同士を掛け合わせ、必要に応じて約分します。

手順：

例：2⁄3 × 3⁄5

1. 分子を掛ける：2 × 3 = 6。

2. 分母を掛ける：3 × 5 = 15。

3. 結果：6⁄15。

4. 約分：両方を3で割って2⁄5。

既約分数や不適切分数でも同様です。

別の例：5⁄8 × 4⁄10

1. 分子：5 × 4 = 20。

2. 分母：8 × 10 = 80。

3. 合計：20⁄80。

4. 約分：20で割って1⁄4。

掛け算前に交差約分すると計算がさらに簡単になります：6⁄10 × 5⁄9

• 分母10と分子5が共通因数を持つ。

• 5⁄10 を1⁄2に約分。

• 残りは6⁄2 × 1⁄9 = 3 × 1⁄9 = 3⁄9 = 1⁄3。

1未満の分数同士を掛けると常に結果は小さくなります。例：¾ × ½ = ⅜。

分数の割り算

割り算は掛け算にもう一手順加えたものです。第2の分数を逆数にしてから掛け算します。

「逆数にして掛ける」ルールは、分数で割ることがその逆数を掛けることと同義だからです。

例：¾ ÷ ½

1. 最初の分数はそのまま：¾。

2. 2番目の分数を反転：½→²⁄₁。

3. 掛け算：¾ × ²⁄₁ = ⁶⁄₄。

4. 約分：2で割って³⁄₂。

5. 必要なら帯分数で1½に。

別の例：⁵⁄₆ ÷ ¹⁰⁄₉

1. ¹⁰⁄₉ を反転して⁹⁄₁₀。

2. 掛け算：⁵⁄₆ × ⁹⁄₁₀ = ⁴⁵⁄₆₀。

3. 約分：15で割って¾。

1未満の分数で割ると答えは大きく、1以上の分数で割ると小さくなるのが一般的です。

実例：レシピで¾カップの材料を半分にしたいときは、¾ ÷ 2 = ¾ × ½ = 3⁄8カップを使います。

覚えておくべきポイント：分数の割り算で通分は不要です。常に2番目を反転して掛けるほうが速くて正確です。

分数計算とより大きな数学の関係

分数は学校で習うだけのものに思えますが、実は身の回りのあらゆるところに潜んでいます。分数の足し算、引き算、掛け算、割り算を行うとき、気づかぬうちに日常や高度な数学の基本概念を使っています。

例えば：

• 比とレシピ：⁸⁄₁₂ を ²⁄₃ に約分すると、それは単なる簡単化ではなく比率の表現です。この比率を使えばクッキーのレシピを2倍にしたり、半量に調整したりできます。

• 名前は怖くない代数：x ÷ ¾ = 2 のような問題は、¾ を⁴⁄₃ に反転して掛ける、分数の割り算と同じトリックです。

• 実用的な単位変換：華氏と摂氏の変換式には⁵⁄₉ が登場しますし、mph を m/s に換算するときも分数が活躍します。

• 確率と可能性：サイコロを振って4が出る確率は¹⁄₆。複数イベントの確率を計算するときも分数の足し算や掛け算が使われます。

分数は中央に線が入った数字以上の存在です。物事の関係性やスケール変化を明確にしてくれるツールであり、活用頻度が高いほど「宿題」ではなく使いこなすショートカットだと感じられます。

豆知識：古代エジプト人は分子を常に1にした表現法を使い、²⁄₃は½ + ¹⁄₆と書いていました。確かに動作しましたが、現代の分数表記のほうがずっと見やすいですね。