直角三角形計算ツール

直角三角形とは

直角三角形とは、1つの角がちょうど90°の三角形のことです。その直角に接する2つの辺はそれぞれ「脚」と呼ばれ、角の向かい側にある最も長い辺は「斜辺」と呼ばれます。多くの公式では、脚をaとb、斜辺をcと表記します。

直角三角形は屋根の傾斜や橋の支柱、街灯の影など、ほぼあらゆる所で見られます。数学で好まれる理由は、少ない数字で欠けている辺や角を簡単に計算できるためです。

直角三角形の特徴は、3辺の間に成立する自明な関係性にあります。ピタゴラスの定理のおかげで、2辺がわかれば常に残りの1辺を求めることができるのです。そのため、直角三角形は基礎幾何学から三角法、物理学まであらゆる分野の土台となっています。

直角三角形の計算方法

直角三角形にはシンプルなルールがあります：a² + b² = c²

これはピタゴラスの定理で、2つの脚（a と b）と斜辺（c）を結びつけます。2辺がわかれば常に3辺目を計算できます。

例えば、脚が3と4のとき、斜辺は以下のように求められます：

c = √(3² + 4²) = √(9 + 16) = 5

この3-4-5の三角形は数値がシンプルなためよく知られていますが、同じルールは小数や大きな値の直角三角形にも適用できます。

また、欠けている脚を求めるには公式を次のように変形します：

• a = √(c² − b²)

• b = √(c² − a²)

これらの簡略化された形で、手作業でも計算ミスなく素早く確認できます。

直角三角形の角度を求める方法

辺の長さがわかれば、三角関数を用いて角度も簡単に求められます。代表的な方法は次の通りです：

• タンジェントを使う：θ = arctan(a⁄b) — 脚の長さ両方がわかるときに便利です。

• サインを使う：θ = arcsin(a⁄c) — 脚の長さと斜辺がわかるときに役立ちます。

これらの関数で欠けた角度がすぐにわかります。一方の鋭角がわかれば、もう一方は90° − θで求められます。

計算結果の確認やさらなる学習には、三角関数計算ツールもぜひご活用ください。

直角三角形の周囲と面積

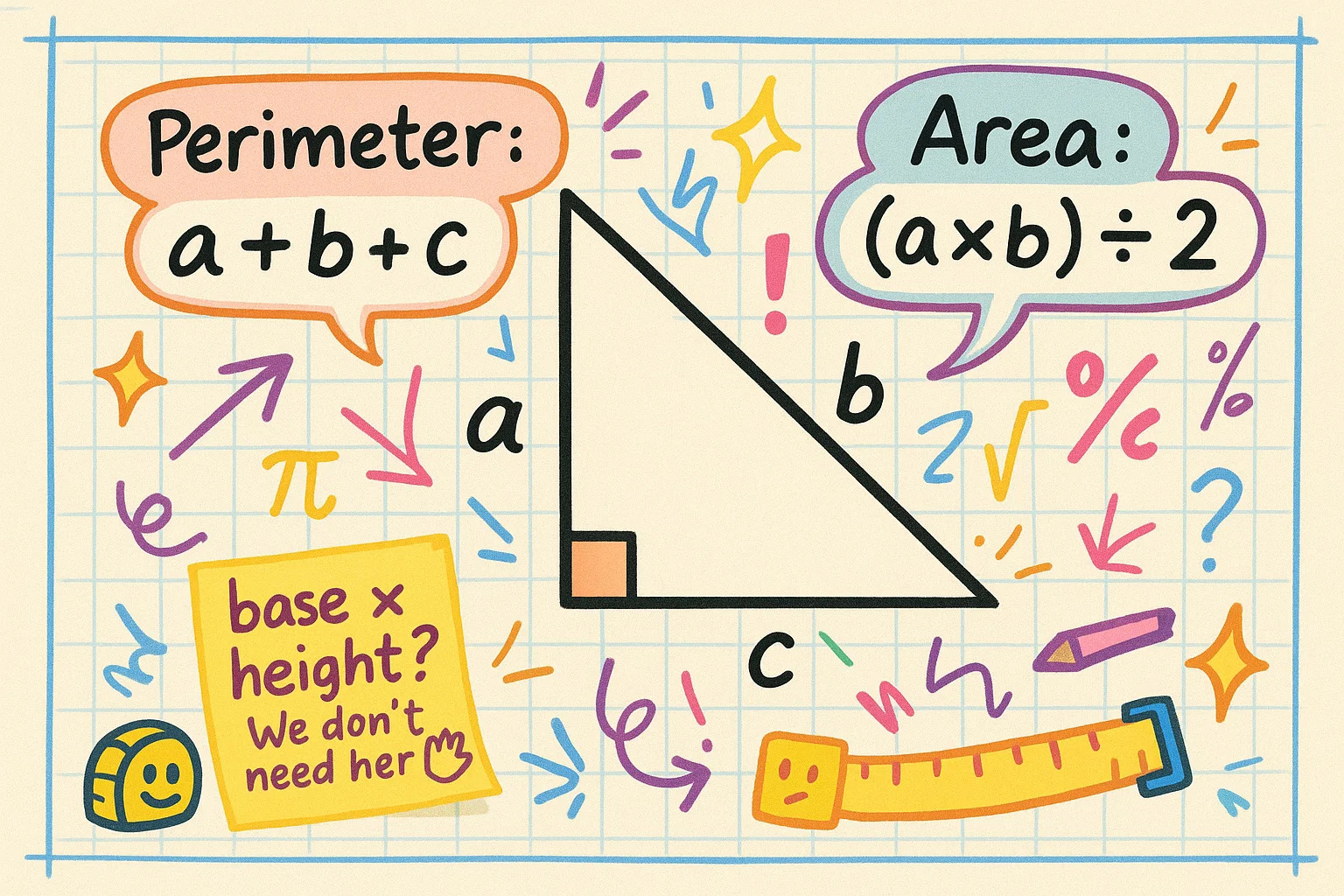
辺がわかれば、直角三角形の周囲の長さと面積もすぐに求められます。周囲は3辺の合計です：P = a + b + c

面積は直角をなす2つの脚が底辺と高さになるため、以下で簡単に計算できます：A = (a × b) ÷ 2

例えば、脚が6と8の場合、斜辺はピタゴラスの定理より10です。周囲は6 + 8 + 10 = 24で、面積は(6 × 8) ÷ 2 = 24となります。

これらの公式で宿題や建築計画、DIYプロジェクトなどで三角形のサイズをすばやく把握できます。

よく使われる直角三角形の比率

数学や実生活で頻繁に出てくる直角三角形は、「特別な三角形」と呼ばれ、固定された辺の比率があるため、追加の計算をせずにすぐに辺や角を求められます。

代表的なものは次の2つです：

1. 30°–60°–90°の三角形

• 辺の比は常に1 : √3 : 2です。

• 最も短い辺（30°の向かい側）を基準として、斜辺はその2倍、もう一方の脚は√3倍となります。

• 両脚は等しく、斜辺は脚の長さの√2倍です。

• 比率は1 : 1 : √2となります。

これらのパターンを覚えておくことで、幾何学や三角法の問題を効率よく解けます。

さらに三角形問題を練習したい方は、 数学計算ツール、ピタゴラスの定理計算ツール、三角関数計算ツールもぜひご利用ください。