惑星の軌道から優雅な建築のドームまで、楕円の面積は目立たないものの、私たちが周囲の世界を理解し形づくる上で重要な役割を果たしています。日常的に計算する機会は少ないかもしれませんが、デザインプロジェクトに取り組むときも、造園を計画するときも、幾何学の問題に挑むときも必要になります。このガイドでは楕円の面積計算ツールの使い方を解説し、歴史的な実例を紹介し、さらにこの楕円形が陸上競技から建築に至るまであらゆる場面で登場する理由を明らかにします。優雅に空間を測定する準備ができているなら、ここが最適です。
楕円の面積とは?
簡単に言えば、楕円の内部を囲む面積、つまり伸びた円のような形の表面積です。完全な円が一つの半径で定まるのに対し、楕円は二つの軸で定義されます。長い方を半長軸(semi-major axis)、短い方を半短軸(semi-minor axis)と呼び、これらによって特徴的な曲線が形づくられます。
楕円は理論上だけのものではありません。天文学では惑星の軌道を表し、工学では部品の形状や力の分布を導く指針となり、デザインでは家具や鏡、床のレイアウト、さらには円形劇場にも取り入れられています。
競技用トラックの楕円形コースから大聖堂の設計まで、楕円の面積は形と機能の両方を現実世界に結びつけます。
長方形、円、不規則形状など他の図形タイプでは、面積計算ツールですべてをひとまとめにして便利に利用できます。同様のツールは数学ツールセクションに揃っており、幾何学・代数・実践的な測定を簡素化するよう設計されています。
楕円の面積を求める公式
幸いなことに、楕円の面積は思ったより簡単に求められます。公式は次の通りです。
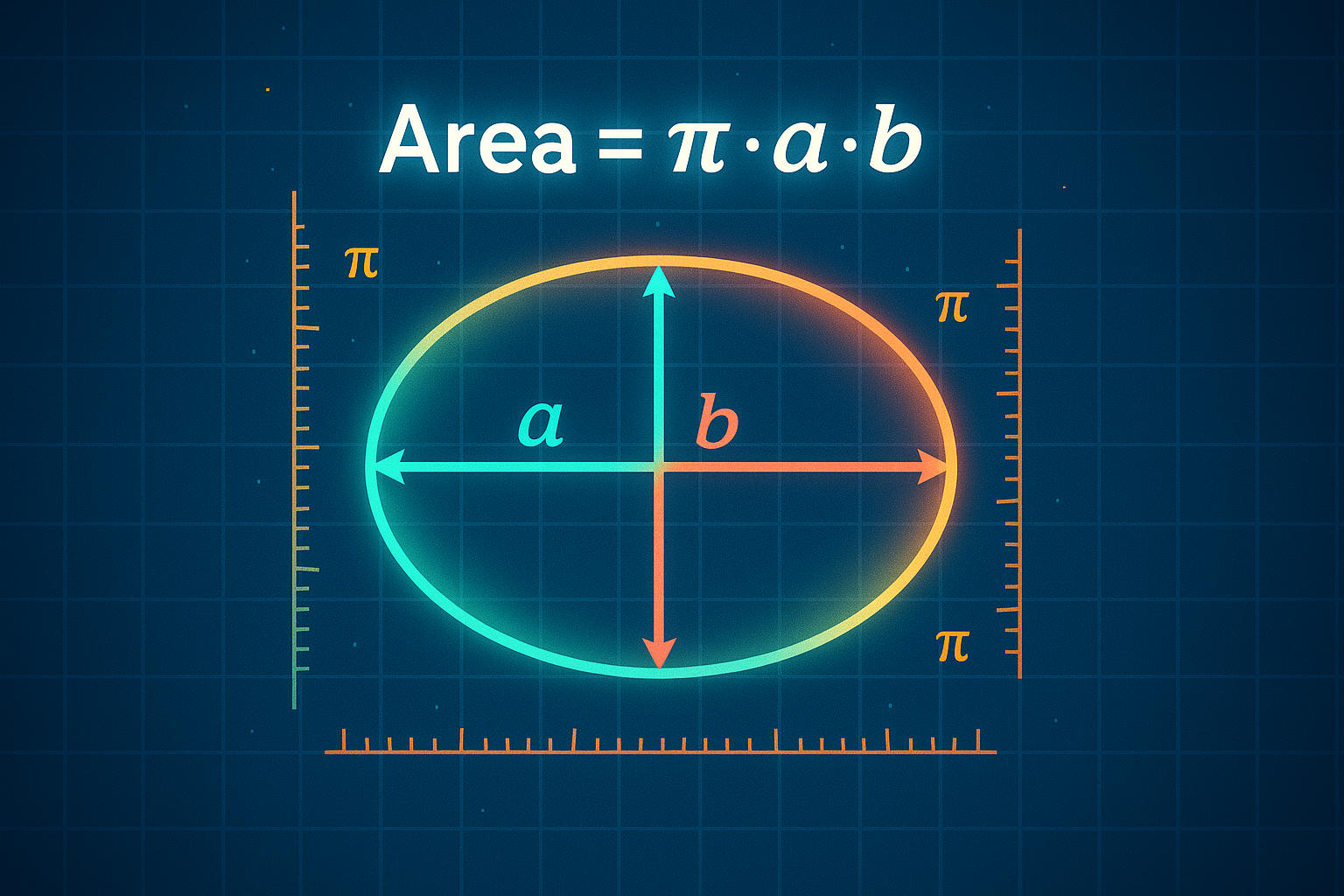
面積 = π × a × b
ここで:
-
π(パイ)はおよそ3.14159 -
aは半長軸(楕円の最長直径の半分) -
bは半短軸(楕円の最短直径の半分)
言い換えれば、半長軸は楕円の幅を示し、半短軸は高さを示します。これら二つの値を掛け合わせ、さらにπを掛ければ、正確で優雅な面積が得られます。
図形が円の場合は、円の面積計算ツールを使うと素早く正確に求められます。
ウィスパリング・ギャラリー
楕円幾何学の最も魅力的な実世界での応用例の一つが、教科書ではなくロンドンのセントポール大聖堂にあることをご存知でしょうか。象徴的なドームの下に位置する円形の回廊はウィスパリング・ギャラリーと呼ばれ、幾何学が音に変わる場所です。
驚くべきことに、回廊の反対側に100フィート以上離れて立つ二人の訪問者が、壁に向かってささやくと、マイクも反響もないのに相手がはっきり聞き取れます。まさに音が完璧に導かれるからです。
なぜ起こるのかというと、楕円が波を反射する仕組みにあります。楕円の任意の焦点から発せられた音波(または光波)は、曲面で反射してもう一方の焦点へと直接伝わります。この原理は楕円の面積公式が示すように、二つの軸が空間以上のものを定義する例です。音の動きさえ形づくります。
この建築的工夫は偶然ではありません。設計者は楕円数学の力を駆使し、美しい構造だけでなく、何世紀を経た今でも訪問者を驚嘆させる体験を生み出しました。


